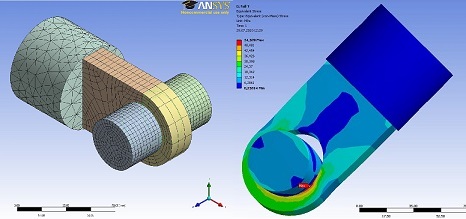
Labor Finite Elemente - Grundlagen
FEM-Grundlagen
Die Methode der finiten Elemente (FEM)
- Die Methode der finiten Elemente (FEM) ist eine numerische Näherungsmethode zur Lösung von Problemen der Ingenieurwissenschaften.
- Ihr Hauptgebiet ist die Festigkeitslehre
- Die FE-Methode eignet sich für Probleme mit komplizierter Geometrie und Belastung oder mit variablen Materialeigenschaften, wenn analytische Lösungen schwer zu realisieren oder ausgeschlossen sind.
- Der Gesamtkörper wird dabei in kleine, aber endliche Teilkörper, die finiten Elemente zerlegt. Diese sind in Knotenpunkten miteinander verknüpft.
- In jedem einzelnen finiten Element werden die unbekannten Feldgrößen durch einfache Funktionen approximiert, die durch ihre Knotenwerte bestimmt sind.
- Die Diskretisierung durch finite Elemente führt auf ein großes Gleichungssystem für die unbekannten Knotenwerte.
Schematischer Ablauf einer FEM-Berechnung
Preprocessing
- Aufteilung des Systems in Finite Elemente
- Die Vernetzung der Problemstellung anpassen
- Bestimmung der Werkstoffkennwerte, der Randbedingungen und der Kräfte
FE-Solver
- Erstellen des Gleichungssystems
- Lösen des Gleichungssystems
- Rückrechnen der Dehnungen, Spannungen und der Reaktionskräfte
Postprocessing
- Erstellen eines Verformungsschaubildes
- Farbliche Kennzeichnung von Dehnungen und Spannungen
- Darstellung von Größe und Richtung der Reaktionskräfte